소수(Prime Number)
- 소수(prime)란 1보다 큰 자연수 중에서 1과 자기자신 이외의 수로는 나누어 떨어지지 않는 수
- 소수의 반대말: 합성수(세 개 이상의 양의 약수를 갖는 자연수)
- 6은 1, 2, 3, 6으로 나누어떨어져서 소수가 아니다.
- 7은 1과 7을 제외하고는 나누어떨어지지 않아서 소수이다.
소수 판별기
1) 2부터 주어진 수 n-1까지의 모든 수를 순회하면서 이 중에서 n의 약수가 있는지 확인하고, 약수가 없다면 소수
- 하나의 수에 대해서 소수인지 아닌지 판별하는 방법
- 2부터 n-1까지 모든 수를 다 확인하기 때문에 시간이 많이 걸린다. 알고리즘의 시간 복잡도는 O(N)
class Main {
public static boolean isPrimeNumber(int num) {
// 1이면 소수가 아니다
if(num == 1) return false;
// 2부터 num을 나누어지게 하는 수가 있으면 소수가 아니다.
for(int i=2; i<num; i++) {
if(num%i==0) return false; // num이 해당 수로 나누어떨어지면 소수가 아님
}
return true; // 위 두 조건에 걸리지 않으면 소수다
}
public static void main(String[] args) {
System.out.println(isPrimeNumber(4)); // False
System.out.println(isPrimeNumber(7)); // True
}
}
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
// 0 ~ N까지 수 중 소수를 구하는 반복문
for(int i=0; i<=N; i++) {
isPrime(i);
}
}
// 소수 생성 메서드
public static void isPrime(int num) {
// 0과 1은 소수가 아니므로 종료
if(num<2) {
return;
}
// 2는 소수
if(num==2) {
System.out.print(num + " ");
return;
}
// 소수가 아닐 경우 종료
for(int i=2; i<num; i++) {
if(num%i==0) return;
}
// 위 반복문에서 약수를 갖고 있지 않을 때 소수
System.out.print(num+" ");
return;
}
}*약수의 성질*
- 모든 약수가 가운데 약수를 기준으로 곱셈 연산에 대해 대칭을 이룬다.

- 따라서 특정한 자연수의 모든 약수를 찾을 때 가운데 약수(제곱근)까지만 확인하면 된다.(16이 2로 나누어떨어진다는 것은 8로도 나누어떨어진다는 뜻이니까 4까지만 확인가능
2) 2부터 ~ 주어진 수 n의 제곱근(소수점 이하 무시)까지의 모든 자연수에 대해 나누어 떨어지는 약수가 있는 지 판별
import java.util.*;
class Main {
public static boolean isPrimeNumber1(int num) {
if(num == 1) return false; // 1은 소수가 아니다
// Math클래스의 sqrt메서드는 특정값의 제곱근(루트)를 구할 수 있다.(double형)
// 2부터 num의 제곱근까지의 모든 수를 확인해서
for(int i=2; i<=Math.sqrt(num); i++) { // num의 제곱근
if(num%i==0) return false; // num이 해당 수로 나누어떨어지면 소수가 아님
}
return true; // 소수
}
public static void main(String[] args) {
System.out.println(isPrimeNumber(4)); // False
System.out.println(isPrimeNumber(7)); // True
}
}
예제) 제곱근을 이용해서 N이하의 모든 소수 구하는 알고리즘 (1번 + 2번)
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
for(int i=0; i<=n; i++) {
isPrime(i);
}
}
// 소수 생성 메서드
public static void isPrime(int num) {
// 0과 1은 소수가 아니므로 종료
if(num<2) {
return;
}
// 2는 소수
if(num==2) {
System.out.print(num + " ");
return;
}
// 소수가 아닐 경우 종료
for(int i=2; i<=Math.sqrt(num); i++) {
if(num%i==0) {
return;
}
}
// 위 반복문에서 약수를 갖고 있지 않을 때 소수
System.out.print(num + " ");
return;
}
}*다수의 소수 판별*
- 특정한 수의 범위 안에 존재하는 모든 소수를 찾아야 할 때 -> 에라토스테네스의 체 알고리즘 사용
에라토스테네스의 체 알고리즘
- 다수의 자연수에 대해 소수 여부를 판별할 때 사용하는 대표적인 알고리즘
- 에라토스테네스의 체는 N보다 작거나 같은 모든 소수를 찾을 때 사용할 수 있다.
- 특정 숫자의 배수는 소수가 아니라는 법칙에 착안해 2~N까지의 숫자에서 숫자들의 배수를 모두 제거한 뒤 제거되지 않은 숫자를 소수로 판별하는 방식(시간 복잡도는 O(N log(log N)))
- 시간복잡도는 매우빠르지만 각 자연수에대한 소수 여부를 저장해야 해서 메모리가 많이 필요하다.

[초기 단계] 2부터 26까지의 모든 자연수를 나열한다.(N=26)

[1단계] 아직 처리하지 않은 가장 작은 수 2를 제외한 2의 배수는 모두 제거한다.
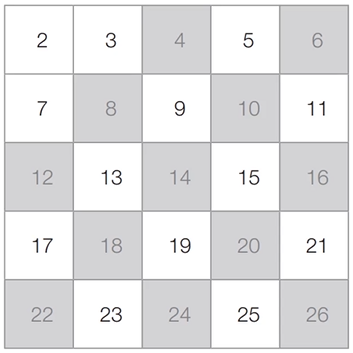
[2단계] 아직 처리하지 않은 가장 작은 수 3를 제외한 3의 배수는 모두 제거한다.
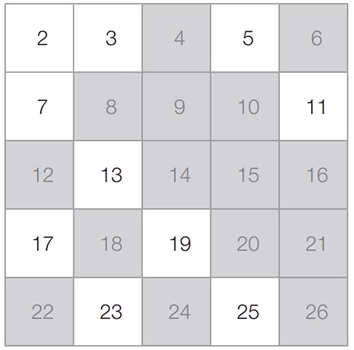
[3단계] 아직 처리하지 않은 가장 작은 수 5를 제외한 5의 배수는 모두 제거한다.
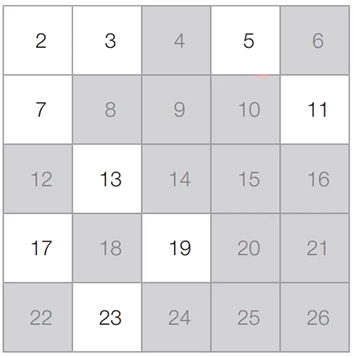
[4단계] 최종적인 결과는 3단계와 같다.
3) 특정 범위에서의 모든 소수를 찾을 때 가장 효율적인 알고리즘(에라토스테네스의 체)
import java.util.Arrays;
public class Main2 {
public static int n = 1000; // 2부터 1000까지의 모든 수에 대하여 소수 판별
public static boolean[] arr = new boolean[n+1];
public static void main(String[] args) {
Arrays.fill(arr, true); // 처음엔 모든 수가 소수(true)인 것으로 초기화(0과 1은 제외)
// 에라토스테네스의 체 알고리즘 수행
for(int i=2; i<=Math.sqrt(n); i++) { // 2부터 n의 제곱근까지의 모든 수를 확인하며
if(arr[i] == true) { // i가 소수인 경우(남은 수인 경우)
// i를 제외한 i의 모든 배수를 지우기
int j = 2;
while(i * j <= n) {
arr[i * j] = false;
j += 1; // 그 다음 인덱스로 넘어가기 위해서
// for(int j=i*i; j<=n; j+=i) {
// arr[j] = false;
}
}
}
for(int i=2; i<=n; i++) // 모든 소수 출력
if(arr[i]) System.out.print(i+" ");
}
}
예제) N 이하의 모든 소수를 구하는 알고리즘 (에라토스테네스의 체를 이용)
import java.util.Scanner;
public class Main {
public static boolean[] prime; // 소수를 체크할 배열
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
make_prime(N);
for(int i=0; i<prime.length; i++) {
if(prime[i]==false) { // 소수(false)일 경우 출력
System.out.print(i + " ");
}
}
}
// N 이하 소수 생성 메서드
public static void make_prime(int num) {
// 소수가 아닌 index = true, 소수인 index = false
prime = new boolean[num+1]; // 인덱스는 0부터 이기 때문에 +1
// 2 미만의 num을 입력받으면 소수는 판별할 필요 xx 바로 return
if(num<2) {
return;
}
prime[0] = prime[1] = true; // 0과 1은 소수가 아님
//제곱근 함수
for(int i=2; i<=Math.sqrt(num); i++) {
if(prime[i]==true) { // 이미 체크된 배열이면 다음 반복문으로 skip
continue; // prime[i]=true와 같다.
}
// i의 배수들을 걸러주기 위한 반복문
for(int j=i*i; j<prime.length; j+=i) {
prime[j] = true; // i의 배수이면 소수가 아니기 때문에 true
}
}
}
}'멀티캠퍼스 풀스택 과정 > 알고리즘' 카테고리의 다른 글
| 알고리즘1-3. 스택(Stack) (0) | 2023.03.29 |
|---|---|
| 알고리즘2-2. 이진탐색알고리즘 (0) | 2022.01.29 |
| 알고리즘2-1. 선형리스트(LinkedList 연결리스트) (0) | 2022.01.27 |
| 알고리즘1-6. 정렬(Sorting): 버블정렬, 선택정렬, 삽입정렬, 퀵정렬 (0) | 2022.01.26 |
| 알고리즘1-5. 재귀알고리즘 (0) | 2022.01.26 |



